Question

When a bactericide is added to a nutrient broth in which bacteria are​ growing, the bacteria population continues to grow for a​ while, but then stops growing and begins to decline.

The size of the population at time t​ (hours) is
`b = 9^6 + 6^4t - 6^3t^2`.
Find the growth rates at t = 0 hours, t = 3 hours, and t = 6 hours.

Answer 1

a) 1296 bacteria per hour

b) 0 bacteria per hour

c) -1296 bacteria per hour

Explanation:

We are given the following information in the question:

The size of the population at time t​ is given by:

`b(t) = 9^6 + 6^4t-6^3t^2`

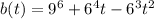
We differentiate the given function.

Thus, the growth rate is given by:

`\displaystyle(db(t))/(dt) = (d)/(dt)(9^6 + 6^4t-6^3t^2)\\\\= 6^4-2(6^3)t`

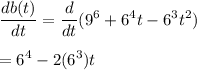
a) Growth rates at t = 0 hours

`\displaystyle(db(t))/(dt) \bigg|_(t=0)= 6^4-2(6^3)(0) = 1296\text{ bacteria per hour}`

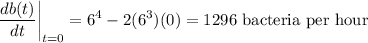
b) Growth rates at t = 3 hours

`\displaystyle(db(t))/(dt) \bigg|_(t=3)= 6^4-2(6^3)(3) = 0\text{ bacteria per hour}`

c) Growth rates at t = 6 hours

`\displaystyle(db(t))/(dt) \bigg|_(t=6)= 6^4-2(6^3)(6) = -1296\text{ bacteria per hour}`