Question

4.One attorney claims that more than 25% of all the lawyers in Boston advertise for their business. A sample of 200 lawyers in Boston showed that 63 of the lawyers had used some form of advertising for their business. At 0.05, is there enough evidence to support the attorney’s claim? (Use the P-value method to test this hypothesis).

Answer 1

`z=\frac{0.315 -0.25}{\sqrt{(0.25(1-0.25))/(200)}}=2.123`

`p_v =P(Z>2.123)=0.0169`

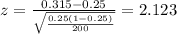
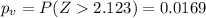
The p value obtained was a very low value and using the significance level given
`\alpha=0.05` we have
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, and we can said that at 5% of significance the proportion of lawyers had used some form of advertising for their business is significantly higher than 0.25 or 25% .

Explanation:

1) Data given and notation

n=200 represent the random sample taken

X=63 represent the lawyers had used some form of advertising for their business

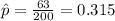`\hat p=(63)/(200)=0.315` estimated proportion of lawyers had used some form of advertising for their business

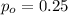`p_o=0.25` is the value that we want to test

`\alpha=0.05` represent the significance level

Confidence=95% or 0.95

z would represent the statistic (variable of interest)

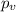`p_v` represent the p value (variable of interest)

2) Concepts and formulas to use

We need to conduct a hypothesis in order to test the claim that more than 25% of all the lawyers in Boston advertise for their business:

Null hypothesis:
`p\leq 0.25`

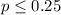
Alternative hypothesis:
`p > 0.25`

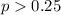
When we conduct a proportion test we need to use the z statistic, and the is given by:

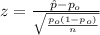`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

The One-Sample Proportion Test is used to assess whether a population proportion
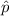`\hat p` is significantly different from a hypothesized value
`p_o`.

3) Calculate the statistic

Since we have all the info requires we can replace in formula (1) like this:

`z=\frac{0.315 -0.25}{\sqrt{(0.25(1-0.25))/(200)}}=2.123`

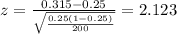
4) Statistical decision

It's important to refresh the p value method or p value approach . "This method is about determining "likely" or "unlikely" by determining the probability assuming the null hypothesis were true of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed". Or in other words is just a method to have an statistical decision to fail to reject or reject the null hypothesis.

The significance level provided
`\alpha=0.05`. The next step would be calculate the p value for this test.

Since is a right tailed test the p value would be:

`p_v =P(Z>2.123)=0.0169`

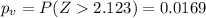
The p value obtained was a very low value and using the significance level given
`\alpha=0.05` we have
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, and we can said that at 5% of significance the proportion of lawyers had used some form of advertising for their business is significantly higher than 0.25 or 25% .