Question

A spring has a force constant k, and an object of mass m is suspended from it. The spring is cut in half and the same object is suspended from one of the halves. How are the frequency of oscillation, before and after the spring is cut, related?

Answer 1

`f2/f1 = √(2)`

Step-by-step explanation:

From frequency of oscillation

`f = 1/2pi *√(k/m)`

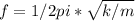
Initially with the suspended string, the above equation is correct for the relation, hence

`f1 = 1/2pi *√(k/m)`

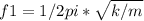
where k is force constant and m is the mass

When the spring is cut into half, by physics, the force constant will be doubled as they are inversely proportional

`f2 = 1/2pi *√(2k/m)`

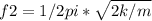
Employing f2/ f1, we have

`f2/f1 = √(2)`