Question

Solve for (x, y, z), if there is a solution to the given system of linear equations:

x - 3y - 2z = -3
3x + 2y - z = 12
-x - y + 4z = 3

Answer 1

x=4, y=1, z=2

Explanation:

System Of 3 Linear Equations

When 3 variables x,y,z are related through 3 independent linear equations, we could find a combination of them which makes the 3 equations become identities. That can be achieved in a very high number of methods.

Let's solve the system of equations shown in the question

`\left\{\begin{matrix}x - 3y - 2z = -3\\ 3x + 2y - z = 12\\ -x - y + 4z = 3\end{matrix}\right`

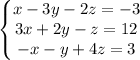
Let's add the first and third equation to eliminate x:

`-4y+2z=0`

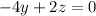
Solving for z

`z=2y`

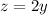
Now we multiply the third equation by 3 and sum it to the second

`\left\{\begin{matrix}3x + 2y - z = 12\\ -3x -3 y + 12z = 9\end{matrix}\right.`

`-y+11z=21`

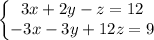
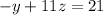
We know that x=2y, so

`-y+11(2y)=21`

`-y+22y=21`

`y=1`

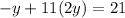
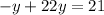
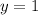
This gives us

`z=2(1)=2`

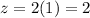
From the very first equation we solve for x

`x=-3+ 3y + 2z`

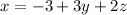
Replacing y=1, z=2, we get

`x=-3+ 3(1) + 2(2)`

`x=4`

The solution is

x=4, y=1, z=2