Question

A study investigated whether regular mammograms resulted in fewer deaths from breast cancer over a period of 20 years. Among 30,615 women who never had​ mammograms, 186 died of breast​ cancer, while only 147 of 30,139 who had undergone screening died of breast cancer. ​a. Do these results suggest that mammograms may be an effective screening tool to reduce breast cancer​ deaths? ​b. If your conclusion is​ incorrect, which type of error did you​ commit?Let p_1 be the proportion of deaths for women who had never had a mammogram and p_2 be the proportion of deaths for women who had undergone screening. Choose the correct null and alternative hypotheses below. a. H0:p1-p2=0 HA:p1-p2>0 b. H0:p1-p2=0 H0:p1-p2≠0c. H0:p1-p2≠0 HA:p1-p2=0d. H0:p1-p2>0 HA:p1-p2<0i. Determine the test statistic. ii. Find the P-value. What is the result of this hypothesis test with a level of significance of 0.1? a. Do not reject the null hypothesis because there is not sufficient evidence to support the claim that screening reduces the proportion of deaths. b. Do not reject the null hypothesis because there is sufficient evidence to support the claim that screening reduces the proportion of deaths. c. Reject the null hypothesis because there is sufficient evidence to support the claim that screening reduces the proportion of deaths. d. Reject the null hypothesis because there is not sufficient evidence to support the claim that screening reduces the proportion of deaths.

Answer 1

Part a

a. H0:p1-p2=0 HA:p1-p2>0

`z=\frac{0.00608-0.00488}{\sqrt{0.00548(1-0.00548)((1)/(30615)+(1)/(30139))}}=2.003`

`p_v =P(Z>2.003)=0.0226`

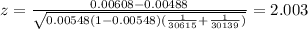
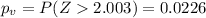
c. Reject the null hypothesis because there is sufficient evidence to support the claim that screening reduces the proportion of deaths.

Because we have a significant proportion of women who died without the screening higher than the proportion of women who died using the screening.

Part b

When the null hypothesis is true (that means that our conclusion was incorrect) and we reject it, we commit a type of error I.

Explanation:

1) Data given and notation

`X_(1)=186` represent the number of women died who had never had a mammogram

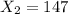`X_(2)=147` represent the number of women died who had undergone screening

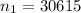`n_(1)=30615` sample of who had never had a mammogram

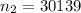`n_(2)=30139` sample of who had undergone screening

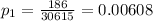`p_(1)=(186)/(30615)=0.00608` represent the proportion of women died who had never had a mammogram

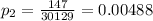`p_(2)=(147)/(30129)=0.00488` represent the proportion of women died who had undergone screening

z would represent the statistic (variable of interest)

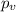`p_v` represent the value for the test (variable of interest)

2) Concepts and formulas to use

We need to conduct a hypothesis in order to check if mammograms may be an effective screening tool to reduce breast cancer​ deaths , the system of hypothesis would be:

a. H0:p1-p2=0 HA:p1-p2>0

Null hypothesis:
`p_(1) \leq p_(2)`

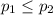
Alternative hypothesis:
`p_(1) > p_(2)`

We need to apply a z test to compare proportions, and the statistic is given by:

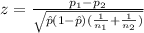`z=\frac{p_(1)-p_(2)}{\sqrt{\hat p (1-\hat p)((1)/(n_(1))+(1)/(n_(2)))}}` (1)

Where
`\hat p=(X_(1)+X_(2))/(n_(1)+n_(2))=(186+147)/(30615+30139)=0.00548`

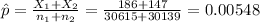
3) Calculate the statistic

Replacing in formula (1) the values obtained we got this:

`z=\frac{0.00608-0.00488}{\sqrt{0.00548(1-0.00548)((1)/(30615)+(1)/(30139))}}=2.003`

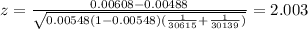
4) Statistical decision

We can calculate the p value for this test.

Since is a one side right tailed test the p value would be:

`p_v =P(Z>2.003)=0.0226`

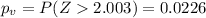
If we compare the p value and the significance level given
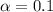`\alpha=0.1` we see that
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis.

c. Reject the null hypothesis because there is sufficient evidence to support the claim that screening reduces the proportion of deaths.

Because we have a significant proportion of women who died without the screening higher than the proportion of women who died using the screening.

b. If your conclusion is​ incorrect, which type of error did you​ commit?

When the null hypothesis is true (that means that our conclusion was incorrect) and we reject it, we commit a type of error I.