Question

The mean rent of a 3-bedroom apartment in Orlando is $1250. You randomly select 13 apartments around town. The rents are normally distributed with a standard deviation of $290. What is the probability that the mean rent is more than $1200?Choose one:

A. 0.2676
B. 0.7324
C. 0.2709
D. 0.7291

Answer 1

B. 0.7324

Explanation:

Population mean (μ) = $1250

Sample size (n) = 13

Sample standard deviation = $290

Assuming a normal distribution, the z-score for any given cost of rent, X, is defined as:

`z = (X-\mu)/((s)/(√(n)))`

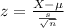
For X= $1200

`z = (1200-1250)/((290)/(√(13)))\\z= - 0.62`

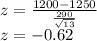
A z-score of -0.62 corresponds to the 26.76-th percentile of a normal distribution. Therefore, the probability that the mean rent is more than $1200 is:

`P(X>1200) = 1 -0.2676 = 0.7324`

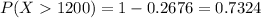
The answer is B. 0.7324