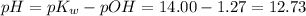Answer:
12.73
Step-by-step explanation:
Write the balanced equation first:
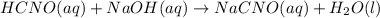
Find moles of the acid (subscript of 1 for simplicity):
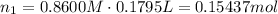
The number of moles of NaOH at the equivalence point will be the same, as we have a 1 : 1 stoichiometry (use subscript of 2 for NaOH):
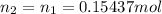
Find the equivalence volume of NaOH:
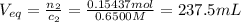
Since we're looking at an instant where we actually add a total of 274.6 mL, this is much greater than the equivalence volume, so we'll have a huge excess of NaOH and we can ignore any ionization of the acid, as it'll be negligible compared to the hydroxide concentration.
Find the excess volume of NaOH added past the equivalence point:
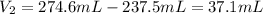
Find the molarity of excess NaOH using the dilution formula (we're dividing by a total volume of this solution):
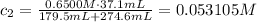
Find the pOH value:
![pOH = -log[NaOH] = -log(0.053105) = 1.27](https://img.qammunity.org/2020/formulas/chemistry/college/raj8q7sddq57n4yd7nlajnno7h9yxy0zgx.png)
Then: