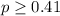Question

Based on the Nielsen ratings, the local CBS affiliate claims its 11:00 PM newscast reaches 41 % of the viewing audience in the area. In a survey of 100 viewers, 36% indicated that they watch the late evening news on this local CBS station.

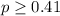
1. What is the alternate hypothesis?
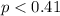
2. What is the sample proportion?
3. What is the critical value if a = 0.01 ?
4. What is the z-statistic?
5. What is the critical value if the level of significance is 0.10?
6. What is your decision if a = 0.01
7. What is the null hypothesis?

Answer 1

1) Null hypothesis:
`p\geq 0.41`

Alternative hypothesis:
`p < 0.41`

2)
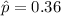`\hat p=0.36` estimated proportion of people indicated that they watch the late evening news on this local CBS station

3)
`z_(crit)=-2.33`

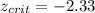
And we can use the following excel code to find it: "=NORM.INV(0.01,0,1)"

4)
`z=\frac{0.36 -0.41}{\sqrt{(0.41(1-0.41))/(1000)}}=-1.017`

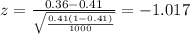
5)
`z_(crit)=-1.28`

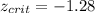
And we can use the following excel code to find it: "=NORM.INV(0.1,0,1)"

6) We see that
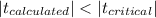`|t_(calculated)|<|t_(critical)|` so then we have enough evidence to FAIL to reject the null hypothesis at 1% of significance.

7) Null hypothesis:
`p\geq 0.41`

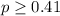
Explanation:

Data given and notation

n=100 represent the random sample taken

X represent the people indicated that they watch the late evening news on this local CBS station

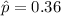`\hat p=0.36` estimated proportion of people indicated that they watch the late evening news on this local CBS station

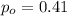`p_o=0.41` is the value that we want to test

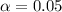`\alpha=0.05` represent the significance level

Confidence=95% or 0.95

z would represent the statistic (variable of interest)

`p_v{/tex} represent the p value (variable of interest)  </p><p><strong>Part 1</strong></p><p>We need to conduct a hypothesis in order to test the claim that 11:00 PM newscast reaches 41 % of the viewing audience in the area:  </p><p>Null hypothesis:[tex]p\geq 0.41`

Alternative hypothesis:
`p < 0.41`

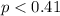
Part 2

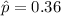`\hat p=0.36` estimated proportion of people indicated that they watch the late evening news on this local CBS station

Part 3

Since we have a left tailed test we need to see in the normal standard distribution a value that accumulates 0.01 of the area on the left and on this case this value is :

`z_(crit)=-2.33`

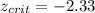
And we can use the following excel code to find it: "=NORM.INV(0.01,0,1)"

Part 4

When we conduct a proportion test we need to use the z statisitc, and the is given by:

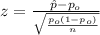`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Since we have all the info requires we can replace in formula (1) like this:

`z=\frac{0.36 -0.41}{\sqrt{(0.41(1-0.41))/(1000)}}=-1.017`

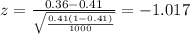
Part 5

Since we have a left tailed test we need to see in the normal standard distribution a value that accumulates 0.1 of the area on the left and on this case this value is :

`z_(crit)=-1.28`

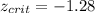
And we can use the following excel code to find it: "=NORM.INV(0.1,0,1)"

Part 6

We see that
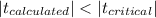`|t_(calculated)|<|t_(critical)|` so then we have enough evidence to FAIL to reject the null hypothesis at 1% of significance.

Part 7

Null hypothesis:
`p\geq 0.41`