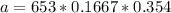Question

Water is discharged from a pipeline at a velocity v (in ft/sec) given by v = 1306p(1/2), where p is the pressure (in psi). If the water pressure is changing at a rate of 0.354 psi/sec, find the acceleration (dv/dt) of the water when p = 36.0 psi

Answer 1

`a=38.5 ft/sec^(2)`

Step-by-step explanation:

Note that acceleration is the rate change of velocity i.e

`acceleration=(change in velocity)/(change in time)\\a=(dv)/(dt) \\`.

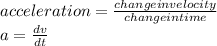Since the velocity is giving as a variable dependent on the pressure, we have to differentiate implicitly both side with respect to time,i.e

`(dv)/(dt)=1306*(1/2)p^(-1/2)(dp)/(dt) \\`

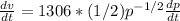
if we substitute value for the pressure as giving in the question and also since the rate change of pressure is 0.354psi/sec, we have

`a=653*0.1667*0.354\\`

`a=(dv)/(dt)=653(36)^(-1/2)*0.354\\  a=38.5 ft/sec^(2)`