Question

The enthalpy of solution of sodium hydroxide is –44.4 kJ/mol. When a 13.9-g sample of NaOH dissolves in 250.0 g of water 23.0 °C in a coffee-cup calorimeter, what is the final temperature of the solution assuming no heat is lost to the surroundings. The solution has the same specific heat of 4.184 J/g-K.

Answer 1

The final temperature of the solution is 9.11 °C.

Step-by-step explanation:

To solve this problem, we can use the equation for heat transfer, q = mcΔT, where q is the heat transfer, m is the mass of the solution, c is the specific heat capacity of the solution, and ΔT is the change in temperature. First, we need to calculate the heat transferred by the sodium hydroxide using the equation q = -44.4 kJ/mol * (13.9 g / 40.0 g/mol). This gives us q = -15.34 kJ. Next, we can use the equation q = mcΔT to calculate the change in temperature. Rearranging the equation, we have ΔT = q / (mc). Plugging in the values, we get ΔT = -15.34 kJ / (250.0 g * 4.184 J/g-K). This gives us ΔT = -13.89 °C. Finally, we can find the final temperature of the solution by adding the ΔT to the initial temperature of 23.0 °C. Therefore, the final temperature of the solution is 9.11 °C.

Answer 2

The final temperature of the NaOH solution: T₂ = 37 °C

Step-by-step explanation:

Given: The enthalpy of NaOH solution:
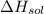`\Delta H_(sol)` = – 44.4 kJ/mol,

The specific heat capacity of solution: c = 4.184 J/g.K

Given mass of solute (NaOH): w = 13.9 g, Molar mass of NaOH: m = 40 g/mol

Mass of the solvent: W = 250 g

Initial temperature of the solution: T₁ = 23 °C = 23 + 273 = 296 K (∵ 0°C = 273 K)

Final temperature of the solution: T₂ = ?

The number of moles of NaOH =
`(given\: mass)/(molar\: mass) = (13.9\, g)/(40\, g/mol) = 0.3475 mol`

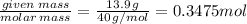
So the amount of heat released (ΔH) by dissolution of 13.9 g NaOH:

`\Delta H = \Delta H_(sol) * n`

`\Rightarrow \Delta H = (- 44.4 kJ/mol) * (0.3475 mol) = 15.429 kJ`

`\Rightarrow \Delta H = 15.429 kJ = 15429 J`

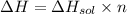
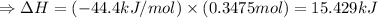
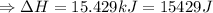
(∵ 1 kJ = 1000J )

Since the specific heat capacity is given by the equation:

`c = (\Delta H)/(M* \Delta T)`

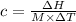
Here, M is the total mass of the solution = w + W = 13.9 g + 250 g =263.9 g

Thus the increase in the temperature (ΔT) can be calculated as:

`\Delta T = (\Delta H)/(M* c)`

`\Rightarrow \Delta T = (15429 J)/(263.9g * 4.184J/g.K) = 13.973`

`\Rightarrow \Delta T = T_(2) - T_(1) = 13.973`

`\Rightarrow \Delta T = T_(2) - 296K = 13.973`

`\Rightarrow T_(2) = 296K + 13.97 = 309.97K = 309.97 - 273^(\circ )C = 36.97^(\circ )C`

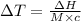
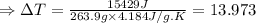
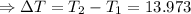
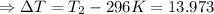
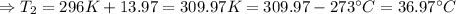
(∵ 0°C = 273 K)

`\Rightarrow T_(2) \approx 37^(\circ )C`

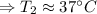
Therefore, the final temperature of the NaOH solution: T₂ = 37 °C