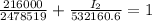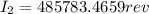Answer:
Radial load of 15 kN, remaining life is 2478519 rev
When load is 25.05, we have 485783 rev
Step-by-step explanation:
For 02-30 mm angular contact bearing, then

Since
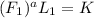 then
then
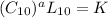
For a ball bearing, a=3 hence
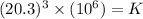
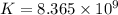
Life at load 15 kN
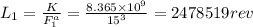
Life load at 25.05 kN

In such a scenario, the Palmgren-Miner cycle ratio summation rule is expressed as
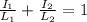
By substitution