Answer:
3.06 x 10^{-5} N
Step-by-step explanation:
mass M1 = 191 kg
mass M2 = 572 kg
mass M3 = 50 kg
distance apart (d) = 0.406 m
gravitational constant (G) = 6.62 x 10^{-11} m^{2}/kg^{2}
Find the magnitude of the net gravitational force exerted by the two larger masses on the 50 kg mas
the net gravitational force acting on the 50 kg mass (M3) = gravitational force exerted by the larger mass (M2) - gravitational force exerted by the smaller mass (M1)
⇒

- y = distance between masses M2 and M3 = 0.406/2 = 0.203
- y1 = distance between masses M1 and M3 = 0.406/2 = 0.203
- y = y1 = 0.203
net force =
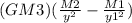
net force =

net force =
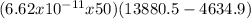
net force = 3.06 x 10^{-5} N