Answer:
Demand is inelastic at p = 9 and therefore revenue will increase with
an increase in price.
Explanation:
Given a demand function that gives q in terms of p, the elasticity of demand is
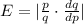
- If E < 1, we say demand is inelastic. In this case, raising prices increases revenue.
- If E > 1, we say demand is elastic. In this case, raising prices decreases revenue.
- If E = 1, we say demand is unitary.
We have the following demand equation
 ; p = 9
; p = 9
Applying the above definition of elasticity of demand we get:
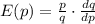
where
- p = 9
- q =
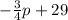
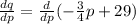
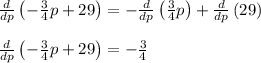
Substituting the values
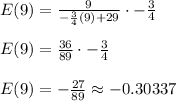
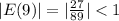
Demand is inelastic at p = 9 and therefore revenue will increase with an increase in price.