Answer:
If the average life is less than 6.24 years, then, it lies in the lower 3% and willing to be replaced.
Explanation:
We are given the following information in the question:
Mean, μ = 10
Standard Deviation, σ = 2
We assume that the distribution of average life is a bell shaped distribution that is a normal distribution.
Formula:
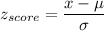
a) P(X<x) = 0.03
We have to find the value of x such that the probability is 0.03.
P(X < x)
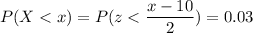
Calculation the value from standard normal z table, we have,
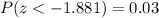
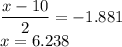
Hence, if the average life is less than 6.24 years, then, it lies in the lower 3% and willing to be replaced.