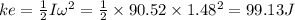Question

A merry-go-round on a playground consists of a horizontal solid disk with a weight of 810 N and a radius of 1.48 m. A child applies a force 50.5 N tangentially to the edge of the disk to start it from rest. What is the kinetic energy of the merry-go-round disk (in J) after 3.05 s?

Answer 1

Kinetic energy will be equal to 99.13 J

Step-by-step explanation:

We have given weight w = 810 N

Radius r = 1.48 m

Time t = 3.05 sec

Acceleration due to gravity
`g=9.8m/sec^2`

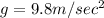
We know that weight is equal to
`w=mg`

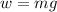
So
`810=m* 9.8`

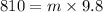
m = 82.65 kg

We know torque
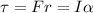`\tau =Fr=I\alpha`, here I is moment of inertia

Moment of inertia is given by

`I=(1)/(2)mr^2=(1)/(2)* 82.65* 1.48^2=90.52kgm^2`

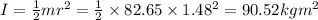
So
`90.52* \alpha =50.5* 1.48`

`\alpha=0.8256rad/sec^2`

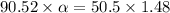
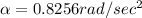
We have given initial angular velocity
`\omega _i=0rad/sec`

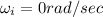
So
`\omega _f=0+0.8256* 3.05=2.518rad/sec`

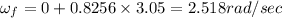
Now rotational kinetic energy is given by

`ke=(1)/(2)I\omega ^2=(1)/(2)* 90.52*1.48^2=99.13J`