Question

A local company wants to evaluate their quality of service by surveying their customers. Their budget limits the number of surveys to 100. What is their maximum error of the estimated mean quality for a 95% level of confidence and an estimated standard deviation of 5?1.8130 1.1550 1.2824 1.3160

Answer 1

Answer: 0.98

Explanation:

Formula to find the maximum error of the mean is given by :-

`E=z*(\sigma)/(√(n))`

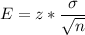
, where n= sample size.

z*= Critical value.

`\sigma` = Population standard deviation

As per given , we have

n= 100

`\sigma= 5`

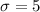
Confidence level : 95%

Critical value for 95% confidence = 1.96 [By z-table ]

Then , the maximum error of the estimated mean quality will be :

`E=(1.96)(5)/(√(100))`

`E=(1.96)(5)/(10)`

`E=(1.96)(1)/(2)=0.98`

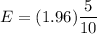
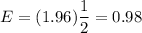
Hence, the required maximum error = 0.98

Thus the correct answer is 0.98 .