Question

Oil with a density of 850 kg/m3 and kinematic viscosity of 0.00062 m2 /s is being discharged by a 5 mm diameter, 40 m long horizontal pipe from a storage tank open to the atmosphere. The height of the liquid level above the center of the pipe is 3 m. Disregarding the minor losses, determine the flow rate of oil through the pipe. Hint: Assume laminar flow and check this assumption at the end.

Answer 1

Flow rate is
`1.82* 10^(-8) m^(3)/s`

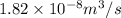
Step-by-step explanation:

Given information

Density of oil,
`\rho_(oil)= 850 Kg/m^(3)`

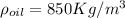
kinematic viscosity,
`v= 0.00062 m^(2) /s`

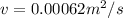
Diameter of pipe, D= 5 mm= 0.005 m

Length of pipe, L=40 m

Height of liquid, h= 3 m

Volume flow rate for horizontal pipe will be given by

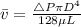`\bar v=\frac {\triangle P\pi D^(4)}{128\mu L}` where
`\mu` is dynamic viscosity and
`\triangle P` is pressure drop

At the bottom of the tank, pressure is given by

`P_(bottom)=\rho_(oil) gh=850 Kg/m^(3)* 9.81 m/s^(2)* 3 m= 25015.5 N/m^(2)`

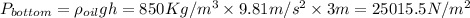
Since at the top pressure is zero, therefore change in pressure a difference between the pressure at the bottom and the top. It implies that change in pressure is still
`25015.5 N/m^(2)`

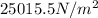
Dynamic viscosity,
`\mu=\rho_(oil)v= 850 Kg/m^(3)* 0.00062 m^(2)/s=0.527 Kg/m.s`

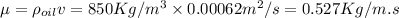
Now the volume flow rate will be

`\bar v=\frac {25015.5 N/m^(2)* \pi * 0.005^(4)}{128* 0.527 Kg/m.s * 40}=1.82037* 10^(-8) m^(3)/s\approx 1.82* 10^(-8) m^(3)/s`

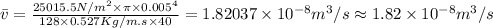
Proof of flow being laminar

The velocity of flow is given by

`V_(flow)=\frac {\bar v}{A}=\frac {1.82* 10^(-8) m^(3)/s}{0.25* \pi* 0.005^(2)}=0.000927104  m/s`

Reynolds number,
`Re=\frac {\rho_(oil) v_(flow) D}{\mu}=\frac {850 Kg/m^(3)* 0.000927104 m/s* 0.005}{0.527 kg/m.s}=0.007476648`

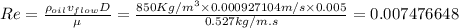
Since the Reynolds number is less than 2300, the flow is laminar and the assumption is correct.