Question

One of the emission spectral lines for Be3+ has a wavelength of 253.4 nm for an electronic transition that begins in the state with n=5. What is the principal quantum number of the lower-energy state corresponding to this emission?

Answer 1

4

Step-by-step explanation:

Relationship between wavenumber and Rydberg constant (R) is as follows:

`wave\ number=R* Z^2(1)/(n_1^2) -(1)/(n_1^2)`

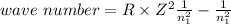
Here, Z is atomic number.

R=109677 cm^-1

Wavenumber is related with wavelength as follows:

wavenumber = 1/wavelength

wavelength = 253.4 nm

`wavenumber=(1)/(253.4* 10^(-9)) \\=39463.3\ cm^(-1)`

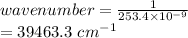
Z fro Be = 4

`39463.3=109677* 4^2((1)/(n_1^2) -(1)/(5^2))\\39463.3=109677* 16((1)/(n_1^2) -(1)/(5^2))\\n_1=4`

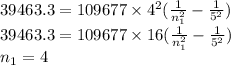
Therefore, the principal quantum number corresponding to the given emission is 4.