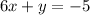What is an equation of the line that passes through the point (-2,7) and is perpendicular to the line x-6y=42 ?

Question

asked Mar 12, 2020 23.9k views

1 Answer

Skytiger · Answer 1 · 2020-03-16T21:47:01+0000

Answer:

The equation of the line that passes through the point (-2,7) and is perpendicular to the line x-6y=42 is

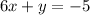
Explanation:

Given:

Let,

point A( x₁ , y₁) ≡ ( -2 , 7)

To Find:

Equation of Line that passes through the point (-2,7) and is perpendicular to the line x-6y=42=?

Solution:

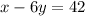x-6y=42 ..................Given

which can be written as

y=mx+c

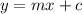
Where m is the slope of the line

∴
y=(x)/(6)-7

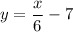
On Comparing we get

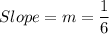
Slope = m = (1)/(6)

The Required line is Perpendicular to the above line.

So,

Product of slopes = - 1

$m* m_(1)=-1\\Substituting\ m\\ (1)/(6) m_(1)=-1\\\\m_(1)=-6$

Slope of the required line is -6

Equation of a line passing through a points A( x₁ , y₁) and having slope m is given by the formula,

i.e equation in point - slope form

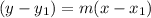
(y-y_(1))=m(x-x_(1))

Now on substituting the slope and point A( x₁ , y₁) ≡ ( -2, 7) and slope = -6 we get

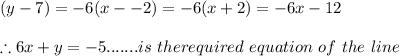
$(y-7)=-6(x--2)=-6(x+2)=-6x-12\\\\\therefore 6x+y=-5.......is\ the required\ equation\ of\ the\ line$

The equation of the line that passes through the point (-2,7) and is perpendicular to the line x-6y=42 is