Answer:
We conclude that average reflectometer reading for a new type of paint is greater than 20
Explanation:
We are given the following in the question:
Population mean, μ = 20
Sample size, n = 13
Alpha, α = 0.05
First, we design the null and the alternate hypothesis
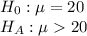
Formula:
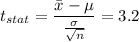
Degree of freedom = n - 1 = 13 - 1 = 12
Now, we calculate the p-value with the help of standard table.
P-value = 0.004
Since, the p-value is less than the significance level, we fail to accept the null hypothesis and reject it.
Thus, there is enough evidence to support that average reflectometer reading for a new type of paint is greater than 20