Answer:
D. 0.9
Step-by-step explanation:
Calculating minimum coefficient of static friction, we first resolve the forces (normal and frictional) acting on the vehicle at an angle to the horizontal into their x and y components. After this, we can now substitute the values of x and y components into equation of static friction. Diagrammatic illustration is attached.
Resolving into x component:
∑
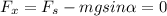
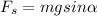 ------(1)
------(1)
Resolving into y component:
∑

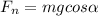 ------(2)
------(2)
Static frictional force,
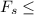 μ
μ
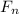 ------(3)
------(3)
substituting
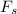 from equation (1) and
from equation (1) and
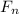 from equation (2) into equation (3)
from equation (2) into equation (3)
 μ
μ
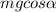
 μ
μ
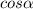
μ
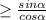
μ
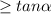
The angle the vehicles make with the horizontal α = 42°
μ ≥ tan 42°
μ ≥ 0.9