Question

Certain neutron stars (extremely dense stars) are believed to be rotating at about 14 revs/s.

If such a star has a radius of 25 km, what must be its minimum mass so that material on its surface remains in place during the rapid rotation?

Answer 1

`1.81263* 10^(27)\ kg`

Step-by-step explanation:

G = Gravitational constant = 6.67 × 10⁻¹¹ m³/kgs²

M = Mass of the star

m = Mass of object at a distance r

r = Radius = 25 km

N = 14 rev/s

The gravitational force of will balance the centripetal acceleration

`(GMm)/(r^2)=(mv^2)/(r)`

Velocity is given by

`v=r\omega`

`(GMm)/(r^2)=(mr^2\omega^2)/(r)\\\Rightarrow M=(r^3\omega^2)/(G)\\\Rightarrow M=(25000^3* (14* 2\pi)^2)/(6.67* 10^(-11))\\\Rightarrow M=1.81263* 10^(27)\ kg`

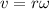
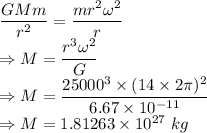
The mass of the neutron star is
`1.81263* 10^(27)\ kg`