Answer:
De broglie wavelength will be 0.727 nm
Step-by-step explanation:
We have given speed of the electron
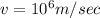
Mass of the electron
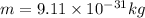
Plank's constant
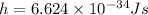
We have to find the De Broglie wavelength
De Broglie wavelength is given by
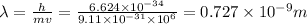
So wavelength will be 0.727 nm