Question

Use Triangle ABC with coordinates A(6,-2),B(-5,3), and C(1,4) to create a translation 3 units left and 2 units up. Write the coordinates of each image in matrix form.

​

Answer 1

c.
`\left[\begin{array}{ccc}3&-8&-2\\0&5&6\end{array}\right]`

Explanation:

Given:

Vertex of triangle:

A(6,-2)

B(-5,3)

C(1,4)

The triangle ABC is translated 3 units left and 2 units up.

To find the co-ordinates of the vertex of the translated triangle in matrix form.

Solution:

Transformation sequence occurring can be given as:

3 units left shift would decrease the x-coordinate by 3 units.

2 units upwards shift would increase y-coordinate by 2 units.

So, we have

`(x,y)\rightarrow (x-3,y+2)`

The Image points will be given as:

`A(6,-2)\rightarrow A'(6-3,-2+2)=A'(3,0)`

`B(-5,3)\rightarrow B'(-5-3,3+2)=B'(-8,5)`

`C(1,4)\rightarrow C'(1-3,4+2)=C'(-2,6)`

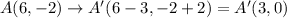
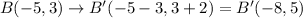
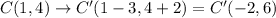
The image points in matrix form can be given as:

`\left[\begin{array}{ccc}A'&B'&C'\\x_1&x_2&x_3\\y_1&y_2&y_3\end{array}\right]`

Plugging in the points the matrix can be written as:

`\left[\begin{array}{ccc}3&-8&-2\\0&5&6\end{array}\right]` (Answer)