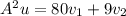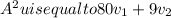
Answer: Option C
Explanation:
Given A is
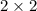 matrix has Eigen values
matrix has Eigen values
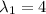 and \lambda_{2}=3 with Eigen vectors
and \lambda_{2}=3 with Eigen vectors
 respectively.
respectively.
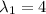 and
and
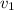 is the eigen vector, substitute this to A so then
is the eigen vector, substitute this to A so then
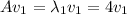
Squaring ‘A’ value ‘4’, we get
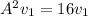
Given
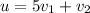 , from this, the above can be written as
, from this, the above can be written as
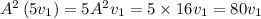
Similarly,
 and
and
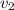 is the eigen vector. Then,
is the eigen vector. Then,
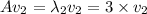
Squaring ‘A’ value ‘3’, we get
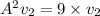
To find
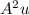 , multiply
, multiply
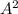 in both sides of the equation
in both sides of the equation
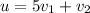 , we get
, we get
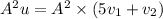
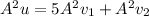
Substitute the value that found above,