Question

The amount of insurance​ (in thousands of​ dollars) sold in a day by a particular agent is uniformly distributed over the interval ​[5​, 70​]. A. What amount of insurance does the agent sell on an average​ day? B. Find the probability that the agent sells more than ​$40​,000 of insurance on a particular day.

A. The agent sells ​$ nothing of insurance on an average day.
B. The probability that the agent sells more than ​$40​,000 of insurance on a particular day is nothing. ​(Round to two decimal places as​ needed.)

Answer 1

a) The agent sells ​37,500$ of insurance on an average day.

b) There is a 53.85% probability that the agent sells more than ​$40​,000 of insurance on a particular day.

Explanation:

An uniform probability is a case of probability in which each outcome is equally as likely.

For this situation, we have a lower limit of the distribution that we call a and an upper limit that we call b.

The probability that we find a value X lower than x is given by the following formula.

`P(X \leq x) = (x - a)/(b-a)`

The mean of this distribution is given by the following formula:

`M = (a+b)/(2)`

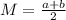
For this problem, we have that:

`a = 5000, b = 70000`

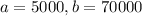
A. What amount of insurance does the agent sell on an average​ day?

`M = (5000 + 70000)/(2) = 37500`

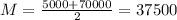
The agent sells ​37,500$ of insurance on an average day.

B. Find the probability that the agent sells more than ​$40​,000 of insurance on a particular day.

`P(X \leq 40000) + P(X > 40000) = 1`

`P(X > 40000) = 1 - P(X \leq 40000) = 1 - (40000 - 5000)/(70000 - 5000) = 0.5385`

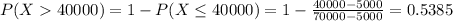
There is a 53.85% probability that the agent sells more than ​$40​,000 of insurance on a particular day.