Answer:
f(5) cannot exceed 30.
Explanation:
f is differentiable in all R, so we can apply the Mean Value Theorem on the interval [0,5], since f is continuous on [0,5] and differentiable on (0,5).
By the MVT, there exists some number c∈(0,5) such that
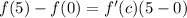 . Substituting the value of f(0), this last equation is equivalent to
. Substituting the value of f(0), this last equation is equivalent to
 . But f'(x)≤7 for all values of x, in particular for x=c, so applying this bound we obtain that
. But f'(x)≤7 for all values of x, in particular for x=c, so applying this bound we obtain that
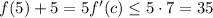 . Then
. Then
 , so substracting 5 from both sides we conclude that
, so substracting 5 from both sides we conclude that
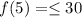 .
.