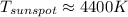Question

The intensity of a sunspot is found to be 3 times smaller than the intensity emitted by the solar surface. What is the approximate temperature of this sunspot if the temperature of the solar surfaceis 5800 K?

a. 4400 K
b. 470,000 K
c. 1900 K
d. 7600 K
e. 1400 K

Answer 1

If the temperature of the solar surface is 5800 K then the approximate temperature of the sunspot is a) 4400 K.

Step-by-step explanation:

The most straightforward way to solve this is using Stefan-Boltzmann law that states that I the energy radiated per unit surface area per unit time (watt per unit area
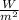`(W)/(m^(2))`) of a black body is proportional to the fourth power of the temperature T of the body:

`I=\sigma T^(4)`

with
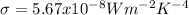`\sigma=5.67x10^(-8) Wm^(-2) K^(-4)` being the Stefan constant.

A black body is an idealized physical body that is a perfect absorber because it absorbs all incident electromagnetic radiation and is also an ideal emitter. The Sun is considered to be a black body at different layers and different temperatures.

We are told that the intensity of a sunspot
`I_(sunspot)` is found to be 3 times smaller than the intensity emitted by the solar surface
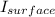`I_(surface)`, that means that:

`I_(sunspot)=(I_(surface))/(3)`

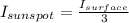
then using the expression of Stefan-Boltzmann law we get that

`\sigma T_(sunspot) ^(4)=\sigma T_(surface) ^(4)`

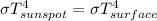
we cross out
`\sigma` and use the fourth root in each side of the equation

`\sqrt[4]{T_(sunspot) ^(4)}=\frac{\sqrt[4]{T_(surface) ^(4)}}{\sqrt[4]{3}}`

`T_(sunspot)=\frac{T_(surface)}{\sqrt[4]{3} }`

then we use that

• 
  `T_(surface)=5800 K`

• 
  `\sqrt[4]{3}\approx1,316`

`T_(sunspot)=(5800 K)/(1,316)`

`T_(sunspot)=4407,3 K`

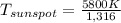
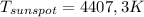
So finally we get that

`T_(sunspot)\approx4400 K`