Question

What is the moment of inertia i of this assembly about the axis through which it is pivoted?

Answer 1

The top answer is correct but it should be mr not mt

Step-by-step explanation:

Answer 2

I =
`(1)/(12)m_t(2x)^2+m_1x^2+m_2x^2`

Step-by-step explanation:

The moment of inertia for the beam is:

I =
`(1)/(12)m_tL^2`

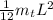
Where
`m_t` is the mass of the beam and L is the lengh of the beam

note:

L = 2x

And for particles I is equal to:

I = MR^2

where M is the mass of the particle and R is the distance between the pivot and the particle.

Finally, the moment of inertia for this assembly is the sum of the moment of inertia of the particles and the beam. So:

I =
`(1)/(12)m_t(2x)^2+m_1x^2+m_2x^2`