Answer:
A baby that is 18 inches long receives a score of -2.
Explanation:
We are given the following information in the question:
The doctor uses 20 inches as a reference point.
Mean, μ = 20 inches
We assume that the distribution of heights of newborn babies is a bell shaped distribution that is a normal distribution.
Formula:
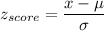
A baby that is 21 inches long receives a score of +1.
Thus, we can write:
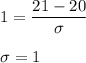
We have to find z-score for baby that is 18 inches long.
Putting x = 18, we get:

A baby that is 18 inches long receives a score of -2.