Question

Only a fraction of the electrical energy supplied to a tungsten light bulb is converted to visible light. The rest of the energy shows up as infrared radiation (i.e., heat). A 75-W light bulb converts 15.0% of the energy supplied to it into visible light. Assuming a wavelength of 550 nm, how many photons are emitted by the light bulb per second? (recall 1 W = 1 J/s)

Answer 1

`n=3.11* 10^(19)\ photons\ per\ second`

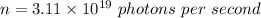
Step-by-step explanation:

It is given that,

Power of the light bulb, P = 75 W

Wavelength,
`\lambda=550\ nm=550* 10^(-9)\ m`

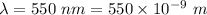
It is mentioned that light bulb converts 15.0% of the energy supplied to it into visible light. 15 % of 75 W is,

`E=15\%\ of \ 75\ W=11.25\ J`

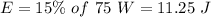
Let n is the number of photons emitted by the light bulb per second. It is given by :

`E=(nhc)/(\lambda)`

`n=(E\lambda)/(hc)`

`n=(11.25* 550* 10^(-9))/(6.63* 10^(-34)* 3* 10^8)`

`n=3.11* 10^(19)\ photons\ per\ second`

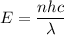
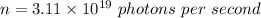
Hence, this is the required solution.