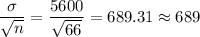Question

The mean annual income for adult women in one city is $28,520 and the standard deviation of the incomes is $5600. The distribution of incomes is skewed to the right. Find the mean and standard error of the mean for this sampling distribution when using random samples of size 66. Round your answers to the nearest dollar.

Answer 1

`E(\bar{x}) = 28520`

Standard error of mean = 689

Explanation:

We are given the following information in the question:

Mean, μ = $28,520

Standard Deviation, σ = $5600

Mean of sampling distribution =

`E(\bar{x}) = \mu = 28520`

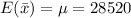
As per Central Limit Theorem, if the sample size is large enough, then the sampling distribution of the sample means follow approximately a normal distribution.

Sample size, n = 66

Since the sample size is large, we can use normal distribution for approximation.

Standard error of mean =

`\displaystyle(\sigma)/(√(n)) = (5600)/(√(66)) = 689.31 \approx 689`