Question

The number of calls coming per minute into a hotel reservation center is Poisson random variable with mean 3.

a) Find the probability that no calls come in a given 1-minute period.
b) Find the probability that at least two calls will arrive in a given two minutes’ period.
c) Find the probability that at most two calls will arrive in a given five minutes’ period.

Answer 1

The probability of various call arrival patterns in a hotel reservation center is calculated using the Poisson distribution. The three parts involve finding the probability of no calls in a minute, at least two calls in two minutes, and at most two calls in five minutes, all based on the Poisson PMF.

Step-by-step explanation:

The given scenario indicates that the number of calls coming per minute into a hotel reservation center is modeled by a Poisson random variable with a mean (λ) of 3. This involves using the Poisson probability mass function (PMF).

Probability of No Calls in a Minute

To find the probability that no calls come in a given 1-minute period (zero calls), we use the PMF formula:

`P(X=k) = (\lambda^k * e^(-\lambda)) / k!`

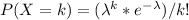
, where X is the Poisson random variable, λ is the average rate (mean), e is the base of the natural logarithm, and k is the number of occurrences (calls).

In this case, for k=0 (no calls), the formula simplifies to

`P(X=0) = (3^0 * e^(-3)) / 0! = e^(-3)`

, which gives us the probability of no calls in a minute.

Probability of At Least Two Calls in Two Minutes

To find the probability of at least two calls in a given two minutes' period, we need to calculate for P(X ≥2) in a two-minute interval. Given the mean rate is 3 calls per minute, the mean for two minutes becomes 3*2=6. We can use the complement rule: P(X ≥2) = 1 - P(X < 2) = 1 - (P(X=0) + P(X=1)).

Probability of At Most Two Calls in Five Minutes

For the probability that at most two calls will arrive in a given five minutes' period, we calculate P(X ≤2) for the interval of five minutes. With the new mean being 3*5=15, we sum up the probabilities for 0, 1, and 2 calls using the PMF.

Answer 2

a) 0.05

b) 0.9826

c) 0.000039308

Step-by-step explanation:

a)
`P_X(0) = (e^(-3)3^0)/(0!) = e^(-3) =  0.05`

b) For two minutes, the mean is doubled, hence it is 6. In order to calculate the probability of al least two calls arriving, we calculate first the probability of the complementary event: At most 1 call will arrive. For that probability, we need to sum the probabilities of 0 and 1.

`P_X(0) = e^(-6)`

`P_X(1) = (e^(-6)*6^1)/(1!) = 6*e^(-6)`

Hence,

`P(X \geq 2) = 1-P(X < 2) = 1- 7*e^(-6) = 0.9826`

c) For five minutes the mean is 15. We need to sum the probabilities of 0, 1 and 2.

`P_X(0) = e^(-15)`

`P_X(1) = e^(15)*15`

`P_X(2) = (e^(-15)*15^2)/(2!) = 112.5*e^(-15)`

As a result,

`P(X \leq 2) = e^(-15)(1+15+112.5) = 0.000039308`

Practically 0