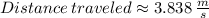Answer:
The total distance that the turtle traveled during the 5 seconds recorded is
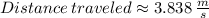
Explanation:
To estimate distance traveled of an object moving in a straight line over a period of time, from discrete data on the velocity of the object, we use a Riemann Sum. If we have a table of values
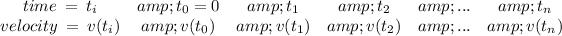
where
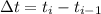 , then we can approximate the displacement on the interval
, then we can approximate the displacement on the interval
![[t_(i-1),t_i]](https://img.qammunity.org/2020/formulas/mathematics/college/3i341gmz3cto555dfom0j54m9etsp9taq6.png) by
by
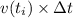 .
.
Therefore the distance traveled of the object over the time interval
![[0,t_n]](https://img.qammunity.org/2020/formulas/mathematics/college/zg4n44eyd71jc96kppvfwilnudh511uto1.png) can be approximated by
can be approximated by
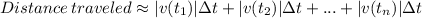
This is the right endpoint approximation.
We are given a table of values for v(t)
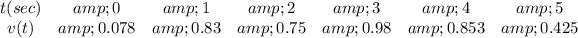
Applying the right endpoint approximation formula we get,
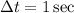
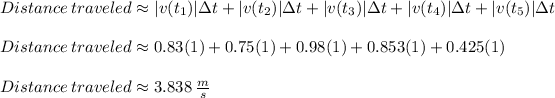
The total distance that the turtle traveled during the 5 seconds recorded is