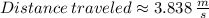Question

The velocity of a turtle is recorded at 1 minute intervals (in meters per second). Use the right-endpoint approximation to estimate the total distance the turtle travelled during the 5 seconds recorded.t (sec): 0 1 2 3 4 5V(t): 0.078 0.83 0.75 0.98 0.853 0.425

Answer 1

The total distance that the turtle traveled during the 5 seconds recorded is
`Distance \:traveled\approx 3.838\:(m)/(s)`

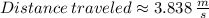
Explanation:

To estimate distance traveled of an object moving in a straight line over a period of time, from discrete data on the velocity of the object, we use a Riemann Sum. If we have a table of values

`\left\begin{array}{ccccccc}time\:=\:t_i&t_0=0&t_1&t_2&...&t_n\\velocity\:=\:v(t_i)&v(t_0)&v(t_1)&v(t_2)&...&v(t_n)\end{array}\right`

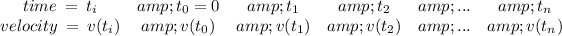
where
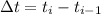`\Delta t=t_i-t_(i-1)`, then we can approximate the displacement on the interval
`[t_(i-1),t_i]` by
`v(t_(i)) *\Delta t`.

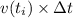Therefore the distance traveled of the object over the time interval
`[0,t_n]` can be approximated by

`Distance \:traveled\approx |v(t_1)|\Delta t+|v(t_2)|\Delta t+...+|v(t_n)|\Delta t`

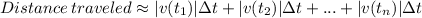
This is the right endpoint approximation.

We are given a table of values for v(t)

`\left\begin{array}{cccccccc}t(sec)&0&1&2&3&4&5\\v(t)&0.078&0.83&0.75&0.98&0.853&0.425\end{array}\right`

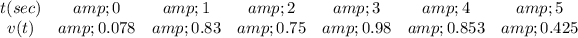
Applying the right endpoint approximation formula we get,

`\Delta t = 1\sec`

`Distance \:traveled\approx |v(t_1)|\Delta t+|v(t_2)|\Delta t+|v(t_3)|\Delta t+|v(t_4)|\Delta t+|v(t_5)|\Delta t\\\\Distance \:traveled\approx 0.83(1)+0.75(1)+0.98(1)+0.853(1)+0.425(1)\\\\Distance \:traveled\approx 3.838\:(m)/(s)`

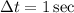
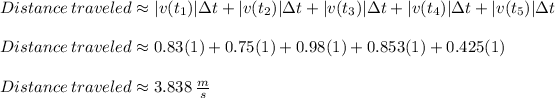
The total distance that the turtle traveled during the 5 seconds recorded is
`Distance \:traveled\approx 3.838\:(m)/(s)`