Answer:
173.45 K
Step-by-step explanation:
This an Adiabatic process because no energy is lost by thermal conduction on expansion. We will be using this Adiabatic condition and ideal gas equation to solve the question.
From idea gas equation;
PV = nRT
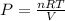 -----(1)
-----(1)
where
P is pressure of the gas
V is volume of the gas
n is number of moles
R is gas constant 8.31441 J K-1 mol-1.
T is temperature in Kelvin
For Adiabatic Condition;
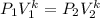 ----(2)
----(2)
Substituting equation(1) into equation(2)
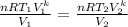
Eliminating the constants and simplify with exponent
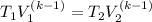
Making T₂ the subject of the formula;
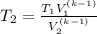
The temperature when the initial volume has quadrupled ⇒ V₂ = 4V₁
⇒
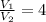
Since air is diatomic, we assume k = 1.4
∴
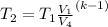
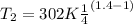
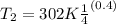
T₂ = 173.45 K