Question

Water is pumped steadily out of a flooded basement at a speed of 5.4 m/s through a uniform hose of radius 0.83 cm. The hose passes out through a window to a street ditch 3.5 m above the waterline. What is the power of the pump?

Answer 1

To solve this problem it is necessary to apply the concepts related to the flow as a function of the volume in a certain time, as well as the potential and kinetic energy that act on the pump and the fluid.

The work done would be defined as

`\Delta W = \Delta PE + \Delta KE`

Where,

PE = Potential Energy

KE = Kinetic Energy

`\Delta W = (\Delta m)gh+(1)/(2)(\Delta m)v^2`

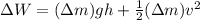
Where,

m = Mass

g = Gravitational energy

h = Height

v = Velocity

Considering power as the change of energy as a function of time we will then have to

`P = (\Delta W)/(\Delta t)`

`P = (\Delta m)/(\Delta t)(gh+(1)/(2)v^2)`

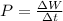
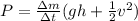
The rate of mass flow is,

`(\Delta m)/(\Delta t) = \rho_w Av`

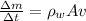
Where,

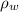`\rho_w` = Density of water

A = Area of the hose
`\rightarrow A=\pi r^2`

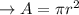
The given radius is 0.83cm or
`0.83 * 10^(-2)`m, so the Area would be

`A = \pi (0.83*10^(-2))^2`

`A = 0.0002164m^2`

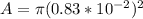
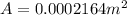
We have then that,

`(\Delta m)/(\Delta t) = \rho_w Av`

`(\Delta m)/(\Delta t) = (1000)(0.0002164)(5.4)`

`(\Delta m)/(\Delta t) = 1.16856kg/s`

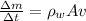
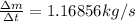
Final the power of the pump would be,

`P = (\Delta m)/(\Delta t)(gh+(1)/(2)v^2)`

`P = (1.16856)((9.8)(3.5)+(1)/(2)5.4^2)`

`P = 57.1192W`

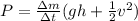
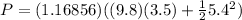
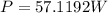
Therefore the power of the pump is 57.11W