Question

Three assembly lines are used to produce a certain component for an airliner. To examine the production rate, a random sample of six hourly periods is chosen for each assembly line and the number of components produced during these periods for each line is recorded. The output from a statistical software package is: SummaryGroups Count Sum Average VarianceLine A 6 250 41.66667 0.266667Line B 6 260 43.33333 0.666667Line C 6 249 41.5 0.7 ANOVASource of Variation SS df MS F p-valueBetween Groups 12.33333 2 6. 166667 11.32653 0.001005Within Groups 8.1666667 15 0.544444Total 20.4999967 17a. Use a .01 level of significance to test if there is a difference in the mean production of the three assembly lines.b. Develop a 99 percent confidence interval for the difference in the means between line B and line C.

Answer 1

a) Reject H₀

b) [0.31; 3.35]

Explanation:

Hello!

a) The objective of this example is to compare if the population means of the production rate of the assembly lines A, B and C. To do so the data of the production of each line were recorded and an ANOVA was run using it.

The study variable is:

Y: Production rate of an assembly line.

Assuming that the study variable has a normal distribution for each population, the observations are independent and the population variances are equal, you can apply a parametric ANOVA with the hypothesis:

H₀ μ₁= μ₂= μ₃

H₁: At least one of the population means is different from the others

Where:

Population 1: line A

Population 2: line B

Population 3: line C

α: 0.01

This test is always one-tailed to the right. The statistic is the Snedecor's F, constructed as the MSTr divided by the MSEr if the value of the statistic is big, this means that there is a greater variance due to the treatments than to the error, this means that the population means are different. If the value of F is small, it means that the differences between populations are not significant ( may differ due to error and not treatment).

The critical region is:

`F_(k-1;n-k; 1-\alpha ) = F_(2;15; 0.99) = 6.36`

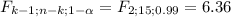
If F ≥ 3.36, the decision is to reject the null hypothesis.

Looking at the given data:

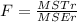`F= (MSTr)/(MSEr)`= 11.32653

With this value the decision is to reject the null hypothesis.

Using the p-value method:

p-value: 0.001005

α: 0.01

The p-value is less than the significance level, the decision is to reject the null hypothesis.

At a level of 5%, there is significant evidence to say that at least one of the population means of the production ratio of the assembly lines A, B and C is different than the others.

b) In this item, you have to stop paying attention to the production ratio of the assembly line A to compare the population means of the production ratio of lines B and C.

(I'll use the same subscripts to be congruent with part a.)

The parameter to estimate is μ₂ - μ₃

The populations are the same as before, so you can still assume that the study variables have a normal distribution and their population variances are unknown but equal. The statistic to use under these conditions, since the sample sizes are 6 for both assembly lines, is a pooled-t for two independent variables with unknown but equal population variances.

t= (X[bar]₂ - X[bar]₃) - ( μ₂ - μ₃) ~t
`_(n_2+n_3-2)`

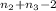
Sa√(1/n₂+1/n₃)

The formula for the interval is:

(X[bar]₂ - X[bar]₃) ±
`t_(n_2+n_3-2; 1 - \alpha /2)`*
`Sa\sqrt{*(1)/(n_2) + (1)/(n_3) }`

`Sa^(2) = ((n_2-1)*S_2^2+ (n_3-1)*S_3^2)/(n_2+n_3-2)`

`Sa^(2) = ((5*0.67)+ (5*0.7))/(6+6-2)`

`Sa^(2) = 0.685`

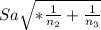
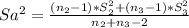
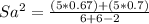
Sa= 0.827 ≅ 0.83

`t_(n_2+n_3-2;1-\alpha /2)= t_(10;0.995) = 3.169`

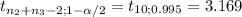
X[bar]₂ = 43.33

X[bar]₃ = 41.5

(43.33-41.5) ± 3.169 *
`*0.83\sqrt{*(1)/(6) + (1)/(6) }`

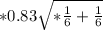
1.83 ± 3.169 * 0.479

[0.31; 3.35]

With a confidence level of 99% you'd expect that the difference of the population means of the production rate of the assemly lines B and C.

I hope it helps!