Question

An Ethernet cable is 4.15 m long. The cable has a mass of 0.210 kg. A transverse pulse is produced by plucking one end of the taut cable. The pulse makes four trips down and back along the cable in 0.765 s. What is the tension in the cable?

Answer 1

95.3 N

Step-by-step explanation:

The tension in the cable is found by the equation:

`T=\mu v^2`

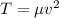
Where
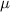`\mu` is the mass density, and
`v` is velocity.

First we find mass density:

`\mu =(m)/(L)` -->
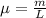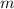`m` is mass:
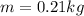`m=0.21kg` and
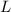`L` is length of the cable:
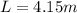`L=4.15m`, so:

`\mu=(0.21kg)/(4.15m) =0.0506kg/m`

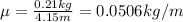
And the velocity:

`v=(distance)/(time) =(d)/(t)`

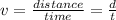
the time is
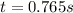`t=0.765s` and in that time the pulse went down and back along the cable 4 times, if one time down and back is:

2*4.15m=8.3m,

four times this path is:

4*8.3m=33.2m

thus, the velocity is:

`v=(distance)/(time) =(33.2m)/(0.765s)=43.4m/s`

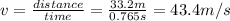
And with this data we can now calculate the tension:

`T=(0.0506kg/m)(43.4m/s)^2\\T=95.3N`

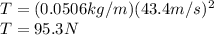
The tension is 95.3N