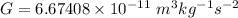Answer:
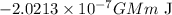
Explanation:
Since, the force of gravity is,

Where,
G = gravitational constant,
M = mass of earth,
m = mass of the particle,
r = distance of particle from centre of the earth,
∵ 7500 km =
 meters
meters
9400 km =
 meters
meters
Thus, work done by the force of gravity,
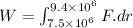
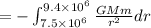
![=GMm[(1)/(r)]_(7.5* 10^6)^(9.4* 10^6)](https://img.qammunity.org/2020/formulas/mathematics/high-school/22dma9qynike26iypv68edgqlv3kginjqb.png)
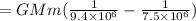
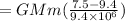
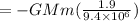
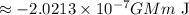
Where,