Question

Melissa has three different positive integers. She adds their reciprocals together and gets a sum of $1$. What is the product of her integers?

Answer 1

The product of the integers is the sum of the products of two different integers , i.e xyz = xy + yz + zx .

Explanation:

Given as :

The sum of the reciprocals of three different integers $1

Let The three different integers are x , y , z

So, The reciprocals of integers =
`(1)/(x)` ,
`(1)/(y)` ,
`(1)/(z)`

Now, According to question

∵ The sum of the reciprocals of three different integers = $1

Or,
`(1)/(x)` +
`(1)/(y)` +
`(1)/(z)` = $1

Now, Taking LCM

I.e
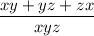`(xy + yz + zx)/(xyz)` = $1

Or, xyz = xy + yz + zx

So, The product of the integers = The sum of the products of two different integers

Hence, The product of the integers is the sum of the products of two different integers , i.e xyz = xy + yz + zx . Answer