Question

A potter’s wheel is a stone disk 90 cm in diameter with mass 120 kg. If the potter’s foot pushes at the outer edge of the initially stationary wheel with a 75-N force for one-eighth of a revolution, what will be the final speed?

Answer 1

To solve this problem it is necessary to apply the concepts related to the theorem of work in angular movement.

Basically, the change in angular kinetic energy must be equivalent to the total angular work done, considering that the work is the Force performed per unit of displacement.

`KE_(f)-KE_(i) = \tau \theta`

`\fra{1}{2}I\omega_f^2-(1)/(2)I\omega_i^2 =\tau\theta`

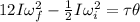
Where

I = Moment of Inertia

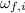`\omega_(f,i)` = Angular velocity (Final and Initial)

`\tau`= Torque

`\theta` = Angular displacement

The moment of inertia of the wheel is given by

`I = (1)/(2)MR^2`

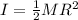
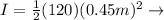`I = (1)/(2) (120)(0.45m)^2 \rightarrow`we have that the diameter was 90cm, then the radius is 45cm or 0.45m

`I = 12.15kg \cdot m^2`

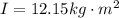
Torque is given by

`\tau = FR`

`\tau = 75*0.45`

`\tau = 33.73Nm`

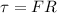
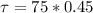
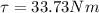
Since the initial angular velocity
`\omega_i` is zero we have that,

`\fra{1}{2}I\omega_f^2=\tau\theta`

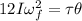
Rearranging to find the final angular velocity we have that

`\omega_f = \sqrt{(2\tau\theta)/(I)}`

`\omega_f = \sqrt{(2(33.75)(0.7854))/(12.15)}`

`\omega_f = 2.09rad/s`

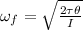
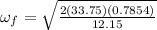
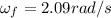
Therefore the final angular velocity 2.09rad/s