Question

The sum of both digits, of either of two two-digit numbers, in whatever order the digits are written, is9. The square of either of the digits of either number, minus the product of both digits, plus thesquare of the other digit is the number 21. The numbers are _______?

Answer 1

The numbers are 45, 54

Solution:

Given a 2 digit number:

a = the 10's digit of the 1st number

b = units digit of the 1st number

From given information,

The sum of both digits, of either of two two-digit numbers, in whatever order the digits are written, is 9

a + b = 9 ---- eqn 1

The square of either of the digits of either number, minus the product of both digits, plus the square of the other digit is the number 21

Square of "a" - product of "a" and "b" + square of "b" = 21

`a^2 - ab + b^2 = 21` --- eqn 2

Let us solve eqn 1 and eqn 2

From eqn 1,

a = 9 - b --- eqn 3

Substitute eqn 3 in eqn 2

`(b - 9)^2 - (9 - b)(b) + b^2 = 21\\\\b^2 + 81 - 18b - 9b + b^2 + b^2 = 21\\\\3b^2 - 27b + 60 = 0`

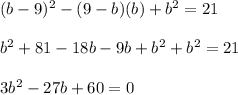
Let us solve the above equation using quadratic formula,

`\text {For a quadratic equation } a x^(2)+b x+c=0, \text { where } a \\eq 0\\\\x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

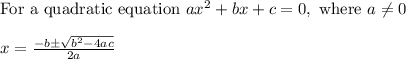
Using the above formula,

`\text{ for } 3b^2 - 27b + 60 = 0 , \text{ we have } a = 3 ; b = -27 ; c = 60`

Substituting the values of a, b, c in above formula,

`\begin{aligned}&b=\frac{-(-27) \pm \sqrt{(-27)^(2)-4(3)(60)}}{2 * 3}\\\\&b=(27 \pm √(729-720))/(6)\\\\&b=(27 \pm √(9))/(6)\\\\&b=(27 \pm 3)/(6)\\\\&b=(27+3)/(6) \text { or } b=(27-3)/(6)\\\\&b=5 \text { or } b=4\end{aligned}`

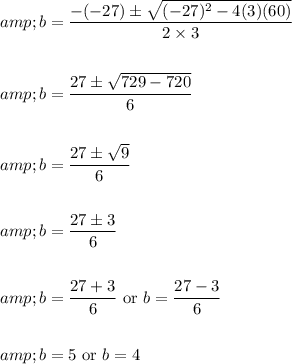
Thus the required numbers are:

when b = 5,

a = 9 - b

a = 9 - 5

a = 4

Thus the number is 45

When b = 4,

a = 9 - b

a = 9 - 4

a = 5

Thus the number is 54