Question

A gas mixture contains equal masses of the monatomic gases argon (atomic mass = 39.948 u) and neon (atomic mass = 20.179 u). These two are the only gases present. Of the total number of atoms in the mixture, what percentage is neon?

Answer 1

To solve this problem it is necessary to apply the relationships given between the number of moles, the atomic mass and the mass of the elements. In general, mass can be expressed in terms of these two terms as:

`n = (m)/(M)`

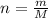
Where,

n = Number of mole

m = Mass

M = Molar mass

Since the mass quantity of the two elements is the same we will have the relation:

`m_(ar)=m_(Ne)=m`

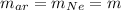
The number of mole of Argon is

`n_(Ar) = (m)/(M_(Ar))`

`n_(Ar) = (m)/(39.38)`

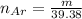
The number of moles of Neon gas is

`n_(Ne) = (m)/(M_(Ne))`

`n_(Ne) = (m)/(20.179)`

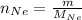
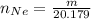
The number of moles of the gas mixture is

`n=n_(Ar)+n_(Ne)`

`n = m((1)/(39.38)+(1)/(20.179))`

`n = 0.075m`

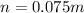
The percentage of the Neon is

`\%Neon=(n_(Ne))/(n)*100\%`

`\%Neon =(0.0495m)/(0.075m)*100\%`

`\%Neon = 66\%`

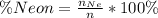
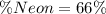
Therefore the percentage of Neon in the gas mixture is 66%