Answer:
The rate of the plane in still air is 1070 km/h and what is the rate of the wind is 220 Km/h
Explanation:
Relative Speeds
If an object moves at a speed
 with respect to another object at a speed
with respect to another object at a speed
 , the relative speeds between them can be
, the relative speeds between them can be
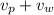 or
or
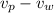 depending if they are collaborative or one against the other.
depending if they are collaborative or one against the other.
The speed of an object who travels a distance x in a time t is

We know that an airplane travels 5100 kilometers in 6 hours when flying against the wind, and travels 3870 kilometers in 3 hours when flying with the wind. Let's call
 and
and
 the speeds of the plane in still air and the wind, respectively. The first travel is performed by the plane with a wind whose speed subtracts from its own, so the relative speed is
the speeds of the plane in still air and the wind, respectively. The first travel is performed by the plane with a wind whose speed subtracts from its own, so the relative speed is
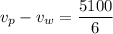
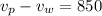
The second travel is performed with the wind pushing in the same direction, so
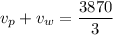
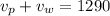
Adding both equations, we have
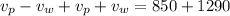
Simplifying and solving

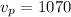
Replacing into the second equation
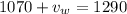

The rate of the plane in still air is 1070 km/h and what is the rate of the wind is 220 Km/h