Question

A country's population in 1992 was 28 million.

In 1999 it was 30 million. Estimate
the population in 2008 using the exponential
growth formula. Round your answer to the
nearest million.
P = Ae^kt
Enter the correct answer

Answer 1

The Estimate for the population in 2008 is 33 million

Explanation:

Exponential Function

Some real-life situations can be modeled by using the exponential function which takes the form

`P = Ae^(kt)`

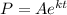
Where A and k are constants, and t is the independent variable.

We are given two data. A country's population in 1992 was 28 million and in 1999 it was 30 million.

Let's express P as the population in million and t the time in years elapsed since 1992.

The information can be written as two points: (0,28), (7,30). Please recall that the second data comes from the year 1999, seven years after the zero reference.

We only have to replace both points in the general form:

`28 = Ae^(k(0))=A(1)=A`

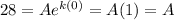
We know A=28 million

Also

`30 = 28e^{k{(7)}}`

`28e^(7k)=30`

`\displaystyle e^(7k)=(30)/(28)`

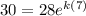
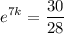
Taking logarithms

`\displaystyle 7k=ln\left ( (30)/(28) \right )`

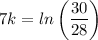
Solving for k

`\displaystyle k=(ln\left ( (30)/(28) \right ))/(7)`

`k=0.00986`

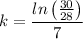
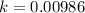
The model is complete now:

`P = 28e^(0.00986t)`

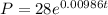
For the year 2008, t=2008-1992=16 years

`P = 28e^(0.00986(16))`

`P = 28(1.1708)`

`P=32.78\ \approx 33`

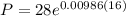
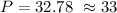
The Estimate for the population in 2008 is 33 million