Answer:
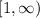
Step-by-step explanation:

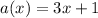
Since we want to know the domain of
 , let's first consider the domain of the inside function, that is, that of
, let's first consider the domain of the inside function, that is, that of
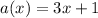 . Every polynomial function has domain all real numbers.
. Every polynomial function has domain all real numbers.
So we can plug anything for function
 and get a number back.
and get a number back.
Now the other function is going to be worrisome because it has a square root. You cannot take square root of negative numbers if you are only considering real numbers which that is the case with most texts.
Let's find
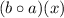 and simplify now.
and simplify now.
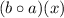
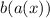
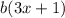
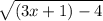
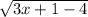
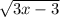
Now again we can only square root positive or zero numbers so we want
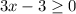 .
.
Let's solve this to find the domain of
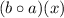 .
.
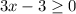
Add 3 on both sides:
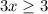
Divide both sides by 3:
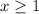
So we want
 to be a number greater than or equal to 1.
to be a number greater than or equal to 1.
The option that says this is
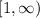
-------------------------------
Give an example why option A fails:
A number in the given set is -2.
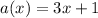

So
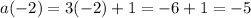 and
and
 .
.
Give an example why option B fails:
A number in the given set is 0.
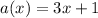

So
 and
and
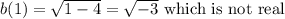 .
.
Give an example why option D fails:
While all the numbers in set D work, there are more numbers outside that range of numbers that also work.
A number not in the given set that works is 3.
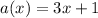

So
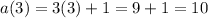 and
and
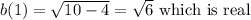 .
.