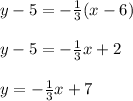Answer:
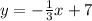
Explanation:
As we know that the line is parallel to the line x+3y=6, we know that it will have the same slope as this equation. To find the slope, we will need to solve for y.
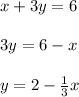
Once we solve for y, we can see that the slope is
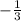
Now that we have the slope and a point, we can use the point-slope formula to find the equation of the line.
This formula says:
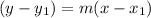
In this formula, m is the slope,
 is the x value of the coordinate pair, and
is the x value of the coordinate pair, and
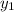 is the y value of the coordinate pair. Knowing this, we can plug in our three known variables into the equation to find the slope of the line.
is the y value of the coordinate pair. Knowing this, we can plug in our three known variables into the equation to find the slope of the line.