Question

The larger of two numbers is twice the smaller increased by five. Find the two numbers if three times the larger exceeds double the smaller by 31

Answer 1

Larger number is 13 and Smaller number is 4.

Explanation:

Let the larger number be x.

Also let the smaller number be y.

We need to find the two numbers.

Given:

The larger of two numbers is twice the smaller increased by five.

framing in equation form we get;

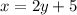`x=2y+5` ⇒equation 1

Also Given:

Three times the larger exceeds double the smaller by 31

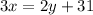`3x=2y+31` ⇒equation 2

Now Substituting the value of x from equation 1 in equation 2 we get;

`3(2y+5) = 2y+31`

Now Using Distributive property we get;

`6y+15 = 2y +31`

Combining the like terms we get;

`6y-2y = 31-15`

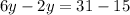
Now Using Subtraction property we get;

`4y =16`

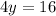
Now Using Division property we get;

`(4y)/(4)=(16)/(4)\\\\y =4`

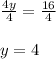
Now Substituting value of y in equation 1 we will find the value of x.

`x=2y+5\\\\x = 2*4+5\\\\x=8+5\\\\x=13`

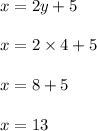
Hence Larger number is 13 and Smaller number is 4.