Question

The cost C (in dollars) of running a gift shop for X days is represented by the equation C=3X +1500. The revenue R (in dollars) is represented by the equation R=600X. How many days will it take for the gift shop to break even?

Answer 1

2.5 days

Explanation:

Costs and Revenues as Functions

We can model economics magnitudes like cost, revenue, profit, and many others as functions. They allow us to explain and predict the behavior of those magnitudes and eventually make decisions over the business.

The gift shop needs C=3X +1500 dollars to run for X days. Besides, the revenue R is R=600X. We need to find the value of X, where the gift shop breaks even (no loss, no profit). We only need to set up the equation

`3X +1500 =600X`

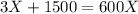
Let's solve for X

`597X=1500`

`X=1500/597=2.5\ days`

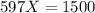
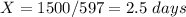
The problem has little sense because 2.5 days is not an adequate value for the number of days. It seems like the Revenue function is wrong. Let's try R=6X:

`3X +1500 =6X`

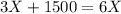
x=500 days

It means that the gift shop needs almost 1 year and 5 months to break even.